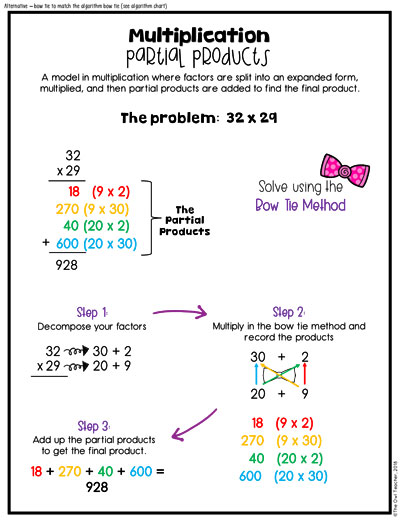
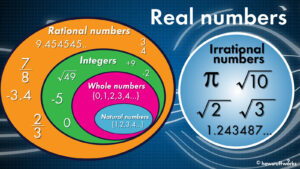
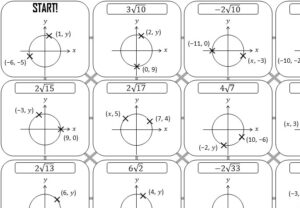
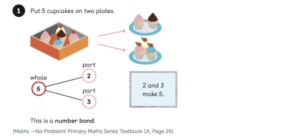
What Strategies Can Be Used to Multiplicate Whole Numbers?

When you learn to calculate the square root of a number, you might not be thinking in terms of what strategies can be used to multiply whole numbers. But for those of you who are, here are some things you need to know. For starters, when you get to the root of a number, it means that all the numbers up to the first number are represented by the same number. And then if the next number is smaller than the first, then the two will cancel each other out.

What are the best strategies to use to multiply whole numbers and find the square root? The best way is to start with a base number. The numbers you choose to work with depend on your purpose. Here are some possibilities:

If you’re working with very small numbers, like say, digits ranging from -2 to 12, the best thing to do would be to find all the roots of the number. These can be found using the method known as cross-product. This involves finding the sum, divided by the prime number (also called a factor). This is a great way of finding the square roots of numbers as they’ll always be either positive or negative. Here’s how you can apply this strategy to finding square roots of the numbers you want to find:

If your number is between zero and one, you’ll need to go through all zeros. You’ll find that the first number has three roots. To make your life easier, you can also make sure your are only looking at the first few digits. If not, you’ll have to do the whole thing backwards. This means you’ll have to go though all zeros one through nine again.

What strategies can be used to multiply whole numbers if you’re dealing with large numbers, say, 4 digits long? Well, let’s do a little trick. All you have to do is multiply each digit individually, then add them together. For example, if your digit is 7, you can multiply it by seven, then by nine, and so on. This will give you your final result, which will in turn give you the square roots.

Another question might be – “How about if I’m not looking for the square roots?” How can you possibly use this when you’re looking for square roots? Well, in this case, you have to multiply each digit independently. Once you have the roots, you can find the actual number. Then you can figure out what the number is and multiply it by itself.

So now, we’ve covered the basics of what strategies can be used to multiply whole numbers. Now, there are other things you can do as well, but these two are probably the most useful. If you have a calculator on your desk, make sure you use it. You can easily plug in numbers that you’re calculating, then check the value right away.

It’s a great way to double check your calculations! Also, make sure your calculator has a memory function so you can go back to previous tables or the results you were getting previously. These two simple tips should be able to answer any question about what strategies can be used to multiply whole numbers.

Now, let’s talk about the second part of the equation. The real answer is not just the product of the quotient and the roots, but also the sum of all the squared roots. This will always be equal to the multiplicative total of all the numbers involved.

What strategies can be used to multiply whole numbers? The best answer is none, unless you want to buy some lottery tickets! For the rest of you, keep on using your calculators. For the square root, if your calculator produces a negative answer, check your math skills. There’s probably a hidden problem somewhere.

Now, we can go on to using the solutions of the quadratic formula and logarithms. These are a little more involved, but the methods are relatively easy. We can also use the solutions of other areas such as geometric forms and algorithms. If you’re interested in trying more than one method, this is an option as well. What strategies can be used to multiply whole numbers can be confusing at first if you don’t know how the formula works. However, once you understand the basics of it, you can start figuring out different methods of application and multiplication in no time.