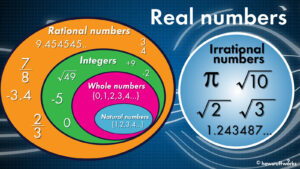
What is the Difference Between Counting Numbers and Whole Numbers?

What is the difference between counting cards and whole numbers? Answer: Yes, the whole numbers 200, 401, and 457 are indeed the whole numbers, which cannot be mixed up with the cards. Answer two: Just identify which are whole numbers from above which are actually counting cards? 6, 8, 5/7.

Answer three: A number system can never be completely exact. We must always make some errors in the application or interpretation of our natural numbers, counting cards included. This is because any object has definite shape and size while numbers don’t.

Question four: How about those irrational numbers, then? For instance, the irrational numbers aren’t even close to the real thing. And so, they cannot be compared to our real numbers at all. Thus, we cannot use these for comparison.

Question five: Can a whole number system be used for calculating irrational numbers? No, because irrational numbers cannot be reduced to their factors. So, they cannot be added, subtracted, or compared with their factors. Clearly, a number system cannot be used for calculating anything. Question six: Why not?

Answer seven: A whole number can only be expressed as a fraction over a given natural number. Decimals, on the other hand, are expressed as a whole number. It follows that a fraction can never be expressed as a whole number. If it were, the denominator would be infinite. So, a natural number can never be compared to a fraction. But a whole number can be compared to a fraction and used as a unit of measurement for computing things such as hours, days, months, and years.

Question eight: Are there any numbers, then, that cannot be reduced to a positive finite number? Yes. And this is just one of the many examples in physics in which what you see is not necessarily what you get.

Question nine: Can the positive integers be computed using a finite number system? Yes, they can. And, since the universe is indeed infinite, then so is the number system. Question ten: Why not?

Thus, we see that while it might be true that decimals and fraction are real types of arithmetic, they do not play a role in the business of real number computing. And that includes counting numbers, as well as natural numbers including zero. Therefore, one does not need to learn or become proficient at decimals and fraction when they do not need to.

Now then, what about counting numbers? Are they really not the same as whole numbers and natural numbers including zero? Well, they are not the same. And it might be a good idea to start off by understanding the difference between them. So let us look at the facts.

For starters, you need to understand that the only numbers that are truly whole are the ones that have no divisors (i.e., zero). And by “whole numbers” we mean those numbers that have no sub-divisions (i.e., zero and even minus one). Therefore, the only real numbers are the ones that include no sub-divisions. Note that when someone mentions “natural numbers,” they are really saying “counting numbers,” not “natural.” The same can be said for “infinity” as well: infinity is not a real number.

When it comes to counting things, though, we do need to use the term “whole number,” as in “two ten-thousandths of a degree.” This type of measurement is usually used in physics, although it has also been used in mathematics and in chemistry. Basically, a fraction is divided into its component parts by adding one to the denominator, which is usually a positive number. This is done so as to get the fraction multiplied by itself a number that adds up to one hundred times its value, or in other words, to get a positive twenty. There are various reasons why a fraction can be divided into its component parts, but the idea behind it is that the parts of the fraction are multiplied together to form a new whole: a positive number.

So how does all of this apply to learning how to count with any precision? In math classes, students learn how to add, subtract, and multiply their way through the alphabet and counting numbers until they have mastered it. By taking the next step and understanding the differences between counting whole numbers versus counting positive integers, students will also see how the math works when dealing with real life situations. For example, in science class, students are expected to solve real-life problems involving mixing chemicals, animals, and plants to come up with new solutions for problems they may encounter. By learning how to multiply these numbers, students gain the tools they need to solve these real-life problems.

As math teachers, it’s important for us to emphasize to our students that real world problems involving fractions and decimals are part of the curriculum, but not the only subjects taught. We teach our students to understand decimals and fraction sums and teach them how to use them to solve problems. By introducing these concepts in the classroom, students begin to develop the ability to separate whole numbers from decimals and the associated factors. Learning decimals and fractions allows students to express different concepts in simple terms that they can understand and make calculations to solve for these decimals and factors later in life.