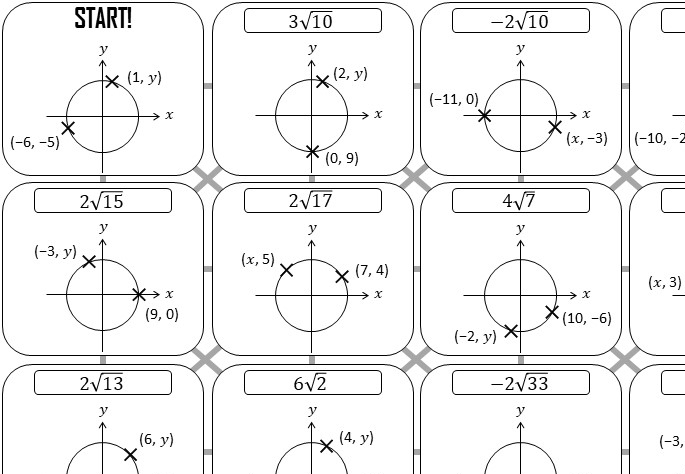
How to divide surds by whole numbers
How to Divide Surds By Whole Numbers If you want to be an effective money manager, then it is essential for

How to Divide Surds By Whole Numbers If you want to be an effective money manager, then it is essential for

What is the Difference Between Counting Numbers and Whole Numbers? What is the difference between counting cards and whole numbers? Answer:
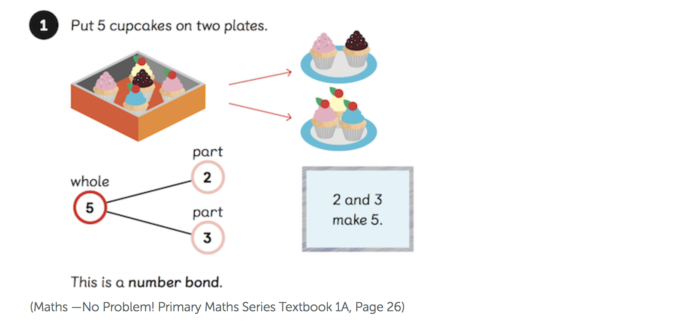
How To Teach Whole Numbers In Primary School You may be one of the many parents who think that learning how

Is the Set of Whole Numbers Closed Under Multiplying? One of the most useful and most fundamental concepts in number theory,

How to Evaluate Expressions With Fractions and Whole Numbers If you are interested in knowing how to evaluate expressions with fractions

What is the Identity For addition of Whole Numbers? In the field of banking, the most used and commonly used digits