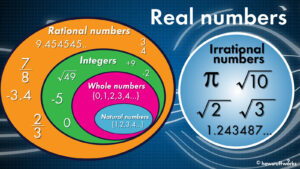
Are Whole Numbers Closed Under Subtraction?
If you have ever seen a math problem, then you have seen the answer written on a piece of paper or on a calculator; the question is, “Are whole numbers closed under subtraction?” The answer is yes, but only under certain conditions. We will discuss these conditions in a moment.

The first condition of the closure property is that the sub-total is always less than the sum of the parts. For example, if A equals B, then A – B is equal to C. Therefore, if we want to know if the subtraction is actually taking place, we must check to see how far along the line A has gone before B is equal to C. If A goes beyond B, then the answer is no, for there is no way that A – B will ever equal C.
The second condition is that the parts of the original sum are equally small. In our example, this means that there are only two integers that are larger than A. To see if this is true, note that the first part of the answer (the part that says A is bigger than B) also has an even number as well. If the second part of the answer is even smaller than A, then we are saying that A is smaller than B when we total A minus B. This is true for all odd numbers, but is especially true for the even ones. Therefore, if we want to know if both A and B are even, then we must conclude that A is smaller than B when we total A minus B.
Now let’s see how this pattern holds true when we also deal with decimals instead of single numbers. The patterns hold true whether we deal with decimals representing a fraction (such as one percent) or multiples of a fraction (such as five percent). Thus, the conclusion follows that the answer we get is also closed, whether we deal with a closed set of real numbers or an open set of real numbers representing a fraction.
The first step in proving this proposition is to demonstrate that any closed set can be decomposed into its components. For this, we need to show that all numbers can be divided into their component sets. We can prove this by starting with the natural numbers. We do this by first noting that any natural number can be divided into either a prime number (that is, a number that is the product of one prime number and one twoth degree smaller than it), or composite numbers such as 2 and 3, which are multiples of prime numbers.
We next note that all rational numbers can be divided into their component sets. By “rationally combining” a pair of real numbers using the formula (where n is the countable number and m the real number), we then have (n m) the quotient part of a real number n. We note that this is a closed system because m cannot be the smaller of n or its prime number, if there are prime numbers between n and m. Thus, when dividing by the smaller factor, we obtain a closed system. This result also follows from the axiom of division by zero, as stated above.
The above proof is adequate for showing the consistency of the above conclusions. But it fails at the most obvious point. It shows that addition and subtraction are valid operations on the natural numbers if the order of their component is closed under partial sums. What is meant by this is that if one adds an element that is greater than zero, then the resulting number will be smaller than zero. And if one subtracts from a number that is less than zero, then the resulting value will be larger than zero. Thus, by the definition of addition and subtraction, the operations are valid on the natural numbers.
However, the above proof is merely a technicality. To know whether the above argument is valid, one needs to know whether the numbers can be added or subtracted without changing their values. For instance, if we take the set of all primes and then add or subtract one from any of their values, such as their square roots, we get a closed set of numbers. Similarly, if we take a closed set of polynomials of degree n and multiply them by any number n such as the product of the first prime and the square root of the first prime, then the resulting polynomial will be closed and therefore, the range of natural numbers which can be added or subtracted to or from is also closed.