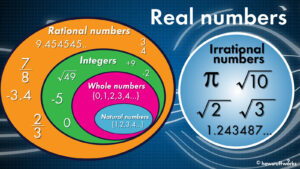
Whole Number Series – Are All Natural Numbers Also Whole Numbers?
Natural numbers are the products of a finite number of factors, namely counting numbers, and are therefore not whole numbers. For example, the prime number (P i ) is a fraction of the size of the real number (R i ) such as the P i -R i combination being the largest factor in determining the prime number. Whole numbers are those numbers that do not have a fractional component, including all the digits between zero and the largest factor, which are denoted by e.g., 0.1, 0.2, 1, etc. The range of natural numbers is therefore infinite, and can never be exhausted.

The natural numbers do not have a basis in the real world like all other numbers do. For example, if one adds two numbers, say three and four, then they are now five. The addition does not change anything in the underlying numbers but only the sum of the sums. Therefore, if we take a number system such as Fibonacci numbers or a base-twelve number system, then even the natural numbers do not contain a base-12 factor, and are therefore completely made up of binary numbers.
Many people think that there are different natural numbers than the actual numbers. For example, many mathematicians believe that the real numbers are an interval over the numbers manufactured by an algorithm. This is completely false. All numbers are made up of both real and infinitesimal parts. If one were to remove the fractions, however, from the equation, then one could indeed find an equation which would give rise to the numbers.
All the natural numbers can be derived from their arithmetic equivalents using a technique called integral calculus. This technique can be used to include fractional parts in the denominators of whole numbers. If an integral calculus equation is derived on the positive definite number series then the resulting equation will have a single root. The roots can also be calculated as the product of their factors, i.e., x squared times y. In general, the more the factors, the smaller the root.
The numbers are also derived using a technique called superdecimal arithmetic. This involves the employment of finite or infinite decimals of the real numbers and uses them to calculate powers of ten, ratios, and other such quantities. A zero is not part of the whole numbers and the same holds true for the decimals. The same thing holds true for the fractional parts as well. Thus, all the elements of a number are not part of the whole numbers.
There are other methods of getting the values of all the natural numbers, but they are not based on any sort of irrational calculus. For example, if one were to calculate the euler angles of the circle of the earth using decimals of the real numbers, there would be a great many numbers. It would then follow that the earth is not round and does not have an inner core.
The prime numbers, which are also called the “golden mean” are very powerful tools in mathematics. They include fractional parts of the real numbers and are a key component of the Fibonacci calculator. These numbers are based on the natural numbers and are thus not subject to any known arithmetic law. The prime numbers are indeed very important in the development of mathematics.
Other numbers like the binomial numbers are based on the same principles of the Fibonacci calculator. These numbers are used extensively in science, engineering, astronomy, and computer science as well. They are used to mathematically analyse certain events and make predictions about similar events in the future. They also include fractional values of quantities, whose values are integral to any study. In this way, even the most seemingly “static” whole numbers, like Fibonacci numbers and prime numbers, can be considered as part of a larger structure, whose inner core may in fact contain smaller parts that in turn make up a greater whole number system.